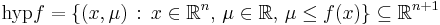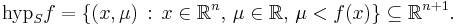Hypograph (mathematics)

In mathematics, the hypograph or subgraph of a function f : Rn → R is the set of points lying on or below its graph:

\mbox{hyp} f = \{ (x, \mu) \,�: \, x \in \mathbb{R}^n,\, \mu \in \mathbb{R},\, \mu \le f(x) \} \subseteq \mathbb{R}^{n%2B1}

and the strict hypograph of the function is:

\mbox{hyp}_S f = \{ (x, \mu) \,�: \, x \in \mathbb{R}^n,\, \mu \in \mathbb{R},\, \mu < f(x) \} \subseteq \mathbb{R}^{n%2B1}.

The set is empty if 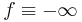f \equiv -\infty .

Similarly, the set of points on or above the function's graph is its epigraph.

Properties

A function is concave if and only if its hypograph is a convex set. The hypograph of a real affine function g : Rn → R is a halfspace in Rn+1.

A function is upper semicontinuous if and only if its hypograph is closed.